Code & Tools

Hands-on tutorial: Granulometric analysis of 21 cm tomography

Hands-on tutorial: Granulometric analysis of 21 cm tomography

This is a hands-on tutorial on the granulometric analysis of 21 cm tomographic data (image or datacube). In-depth discussion on the astrophysical application is described in Kakiichi et al. (2017). This tutorial aims at describing the practical aspects and the python script of the method.

Background: algebra of shapes

First of all, we need to set up a mathematical tool: algebra of shapes. The followings are the well-defined operations in mathematical morphology. The Minkowski addition (dilation) is given by the union of a binary field, X, and a structuring element, S, as the structuring element is moved on the binary field. The diagram below illustrates how this Minkowski sum operation works.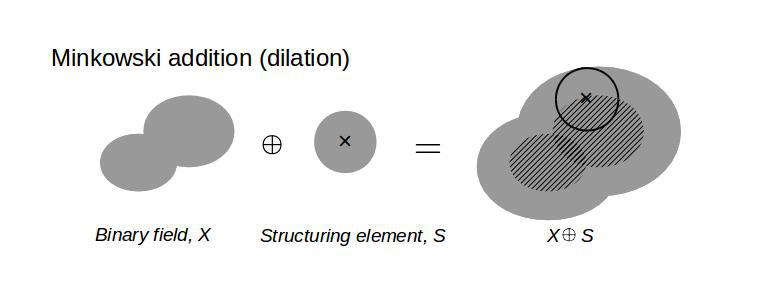
granulometry_dilation
Figure 1. A schematic illustration of the Minkowski addition. The resulting image is shown as the grey area. The shaded region indicates the original image before the operation.
The Minkowski subtraction (erosion) is given by the intersection of a binary field, X, with the centre of a structuring element, S, as the structuring element moves on the binary field. The diagram below illustrates how this Minkowski subtraction operation works.
granulometry_erosion
Figure 2. Minkowski subtraction. The colour coding is same as Figure 1.
The morphological opening is defined by a consecutive operation: Minkowski subtraction followed by Minkowski addition.
granulometry_opening
Figure 3. Morphological opening. The colour coding is same as Figure 1.
The following diagram follows the morphological opening operation step-by-step.
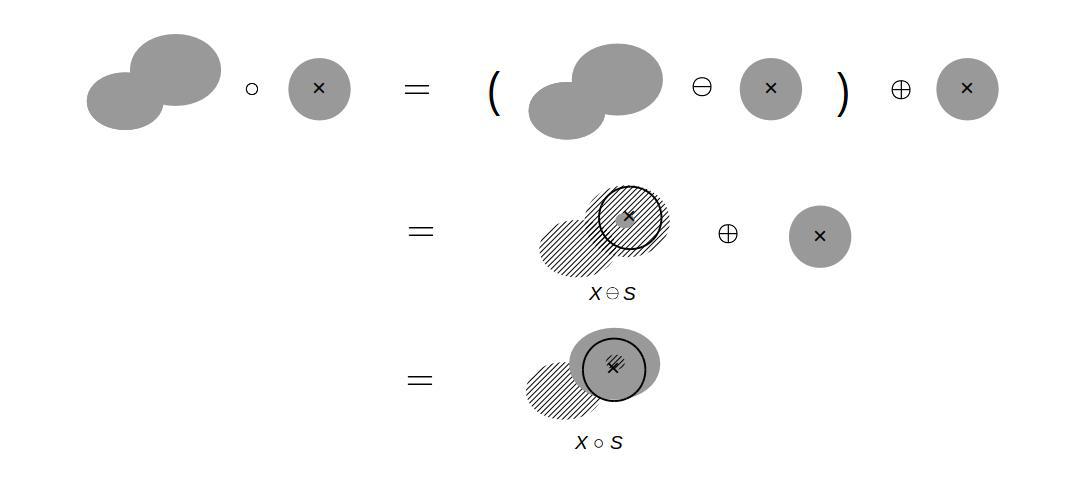
granulometry_opening_step-by-step
The morphological opening can be used as a mathematical abstraction of the concept of sieving. This concept of sieving is the central idea behind the granulometric analysis of images.

Python scripts

Example image: excursion set of a Gaussian random field 
import numpy as np
import scipy.ndimage

Ng=300          # number of cells
smoothing=5     # smoothing scale in pixels
threshold=0.05  # threshold defining the excursion sets of a random field

random_field=np.random.randn(Ng,Ng)
binary_field=scipy.ndimage.gaussian_filter(random_field,sigma=smoothing) > threshold
Thanks to python scipy package (scipy.ndimage, see morphology), the above morphological operations can be implemented very easily (almost one line!). First, we need define the shape of a structuring element, which is used to analyse an image. We take a sphere of radius n in pixels. 
def sphere(n):
    struct = np.zeros((2 * n + 1, 2 * n + 1))
    x, y = np.indices((2 * n + 1, 2 * n + 1))
    mask = (x - n)**2 + (y - n)**2 <= n**2
    struct[mask] = 1
    return struct.astype(np.bool)
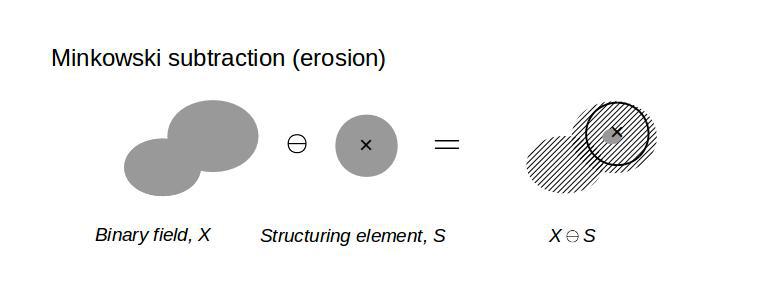
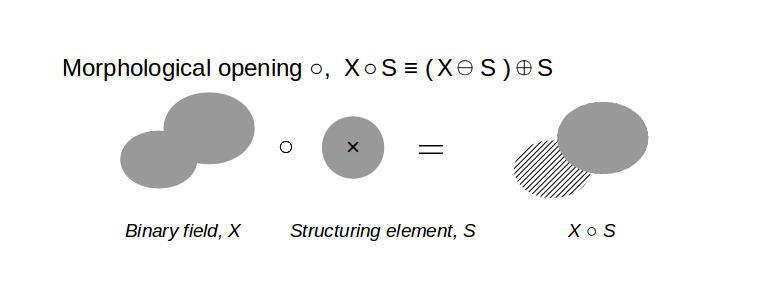
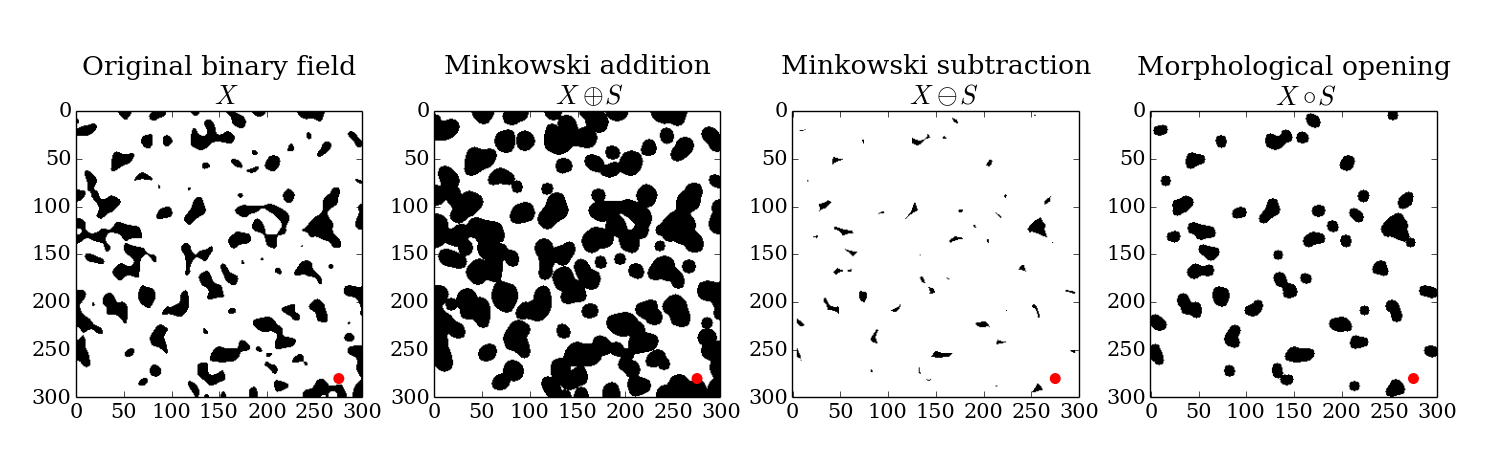
Then, the Minkowski addition, subtraction, and morphological opening of the binary field with the structuring element are simply, 
n=5   # radius of a spherical structuring element in pixels

# Minkowski addition (dilation)
dilation=scipy.ndimage.binary_dilation(binary_field,structure=sphere(n))

# Minkowski subtraction (erosion)
erosion=scipy.ndimage.binary_erosion(binary_field,structure=sphere(n))

# Morphological opening (sieving)
opening=scipy.ndimage.binary_opening(binary_field,structure=sphere(n))
The results of these morphological operations are show in Figure 4.
example
Figure 4. Examples of the Minkowski addition, subtraction, and morphological opening operated on the excursion set of a Gaussian random field. The structuring element is shown as the red circle (n=5 sphere).

Granulometry: size distribution

Granulometry is a method to measure the size distribution of a binary field (2D or 3D) using successive morphological opening operations with varying sizes of a structuring element. An implementation with Python is 
# python script to measure the size distribution of
# a binary 2D image or 3D datacube using a granulometric method

def granulometry(data,dim):    
    def disk(n):
        struct = np.zeros((2 * n + 1, 2 * n + 1))
        x, y = np.indices((2 * n + 1, 2 * n + 1))
        mask = (x - n)**2 + (y - n)**2 <= n**2
        struct[mask] = 1
        return struct.astype(np.bool)
    def ball(n):
        struct = np.zeros((2*n+1, 2*n+1, 2*n+1))
        x, y, z = np.indices((2*n+1, 2*n+1, 2*n+1))
        mask = (x - n)**2 + (y - n)**2 + (z - n)**2 <= n**2
        struct[mask] = 1
        return struct.astype(np.bool)

    s = max(data.shape)
    area0=float(data.sum())
    area=np.zeros(s/2)
    pixel=range(s/2)
    for n in range(s/2):
        print 'binary opening the data with radius =',n,' [pixels]'
        if dim == 2:
            opened_data=scipy.ndimage.binary_opening(data,structure=disk(n))
        if dim == 3:
            opened_data=scipy.ndimage.binary_opening(data,structure=ball(n))
        area[n]=float(opened_data.sum())
        if area[n] == 0:
            break

    pattern_spectrum=np.zeros(s/2)
    for n in range(s/2-1):
        pattern_spectrum[n]=(area[n]-area[n+1])/area[0]

    return (area,pattern_spectrum,pixel)
Usage 
# usage example
dim=2
area,dFdR,pixel=granulometry(binary_field,dim)
R=np.array(pixel) # radius of structural element [pixels]

import matplotlib.pyplot as plt

plt.figure()
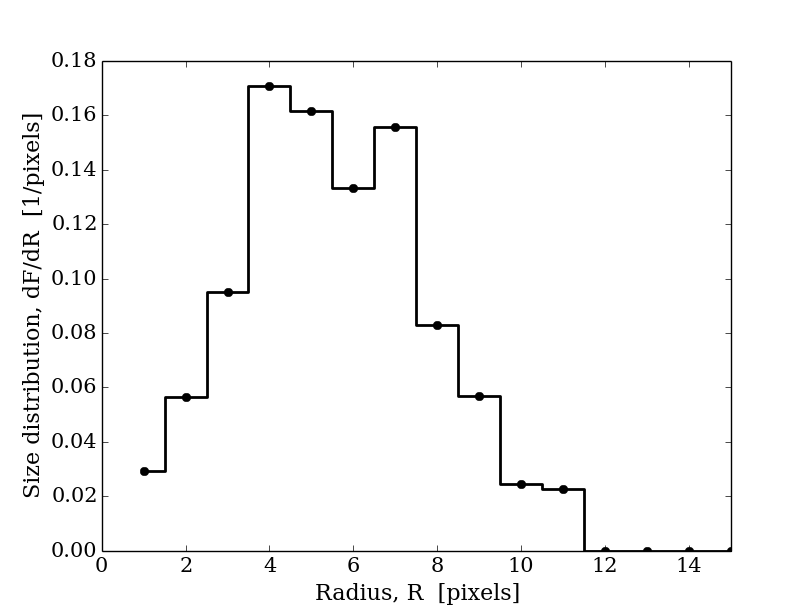
plt.plot(R[1:], dFdR[1:], 'ko-',linewidth=2,drawstyle='steps-mid')
plt.xlabel('Radius, R  [pixels]')
plt.ylabel('Size distribution, dF/dR  [1/pixels]')
plt.xlim(0,15)
plt.show()
size_distribution_example